Written by Tomohiro Iwahashi
§ 今回はR連携を用いて主成分分析(PCA)の可視化をTableauで実施してみたいと思います。
§ 主成分分析とは・・・?
主成分分析とは、多次元データのもつ情報をできるだけ損わずに. 低次元空間に情報を縮約する方法です。
多次元データを2次元(3次元データ)に縮約できれば、データ全体の雰囲気を視覚化することができます。 視覚化によって、調査対象の類似性等、情報を解釈しやすくすることができます。
詳細はこちらを参照ください。
「R」による主成分分析 – 統計科学研究所
www.statistics.co.jp/reference/software_R/statR_9_principal.pdf
今回、解析するデータは都道府県のアルコール消費量で、人口当たりのビール、酒、焼酎、ワイン、ウィスキーの5種類のアルコールの消費量から、都道府県のアルコール消費傾向を探ります。
§ まずはRで分析を実施してみます。
(文字コードをUTF-8化した)テキストデータをR Studioの”Import Dataset”(画面右上Environmentタブ)から読み込みます。Delimiter を Tab, Encoding をDefaultまたはUTF-8とします。
R Studio のコンソールで以下を実行します。
data <- as.data.frame(sakeJ_UTF8) # data frame に変換します
row.names(data) <- data[,1] #1列目(県名)を行の名前に設定します
data = data [,2:6] # 県名を除いたアルコール消費量のデータを入力とします
result = prcomp(data,scale=TRUE) #prcomp関数で主成分分析を行います
result
Standard deviations:
[1] 1.4449807 1.1361589 0.8723427 0.7022989 0.6057791
Rotation:
PC1 PC2 PC3 PC4
人口当たりビール消費量 -0.4861470 0.1988128 0.6080867 -0.5908756
人口当たり酒消費量 -0.5479877 -0.3214838 -0.1853810 0.2388893
人口当たり焼酎消費量 0.4174508 0.5420256 0.3622685 0.2811587
人口当たりワイン消費量 -0.1790259 0.6512052 -0.6648496 -0.3072330
人口当たりウィスキー消費量 -0.5070061 0.3731778 0.1503366 0.6483484
PC5
人口当たりビール消費量 0.07232707
人口当たり酒消費量 0.71057963
人口当たり焼酎消費量 0.56714584
人口当たりワイン消費量 0.08639729
人口当たりウィスキー消費量 -0.40090709
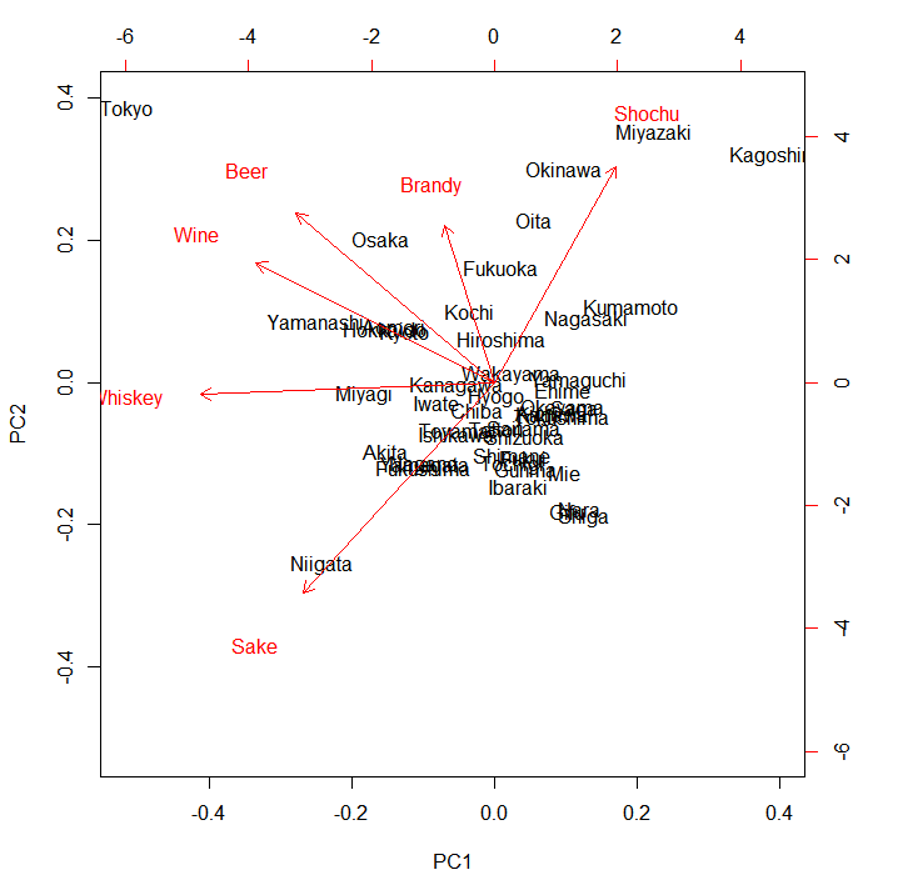
次にbiplot関数に主成分1(PC1)と主成分2(PC2)で2次元のグラフを書きます。
biplot(result)
この結果から横軸(PC1)については、焼酎消費量が多いと正の方向に酒消費量が多いと負の方向に移動する傾向のある軸だとわかります。また、縦軸(PC2)についてはワインの消費量が多いと正の方向に移動する傾向があるようです。
> summary(result)
Importance of components:
PC1 PC2 PC3 PC4 PC5
Standard deviation 1.4450 1.1362 0.8723 0.70230 0.60578
Proportion of Variance 0.4176 0.2582 0.1522 0.09864 0.07339
Cumulative Proportion 0.4176 0.6758 0.8280 0.92661 1.00000
summary(result)を実行すると、主成分の寄与率(どれだけ説明ができるか)を見ることができます。Cumulative Proportion から、PC1とPC2で 67.58%を説明するということが わかります。
result$x[,n] で主成分n の値を返すことができます。
例えば下の例では、それぞれの県の主成分1(PC1)の値を返します。
以降、これを使ってTableauから描画をします。
> result$x[,1]
愛知 愛媛 茨城 岡山 岩手 岐阜
-0.18486496 0.22986099 1.05832236 0.47127026 0.19954491 0.24001969
宮崎 宮城 京都 熊本 群馬 広島
3.59175004 -0.93710420 -0.72927314 2.31869706 1.33865165 -0.61357498
香川 高知 佐賀 埼玉 三重 山形
0.06862214 -1.64799493 0.48168352 1.50910245 0.50347218 -1.62605729
山口 山梨 滋賀 鹿児島 秋田 新潟
-0.19942634 0.41092966 0.81191123 4.23417285 -2.29032150 -3.01962931
神奈川 青森 静岡 石川 千葉 大阪
0.22495553 -1.26407083 0.52430448 -1.35236635 1.53334167 -2.04895194
大分 長崎 長野 鳥取 島根 東京
0.85266898 0.82718172 -0.29840935 -0.83643440 -0.61740533 -3.03653603
徳島 栃木 奈良 富山 福井 福岡
0.46161039 1.15504896 1.30085642 -1.12082616 -0.74800971 0.45715757
福島 兵庫 北海道 和歌山
-0.83525083 -0.05702591 -0.27027402 -1.07132921
§ それでは次にTableauから実行してみます。
+ データソースを読み込みます。
+ PC1 用をRから取得する計算式を作成します。
prcomp1
—————————————-
SCRIPT_REAL(
“n <- max(.arg6)
df <- data.frame(.arg1,.arg2,.arg3,.arg4,.arg5)
pc <- prcomp(df, scale = TRUE)
as.numeric(pc$x[,n])
“,
SUM([人口当たりビール消費量]),
SUM([人口当たり酒消費量]),
SUM([人口当たり焼酎消費量]),
SUM([人口当たりワイン消費量]),
SUM([人口当たりウィスキー消費量]),
1
)
—————————————-
SUM([人口当たりビール消費量]),
SUM([人口当たり酒消費量]),
SUM([人口当たり焼酎消費量]),
SUM([人口当たりワイン消費量]),
SUM([人口当たりウィスキー消費量]) をデータフレームに直し、
prcompに入力し、結果をpc に代入します。
pc$x[,1]はPC1の値を返り値として返します。
最後(.arg6) を2 にすればPC2の値を返します。
+ 同様にして、主成分2(PC2)を返す計算式を作成します。
prcomp2
—————————————-
SCRIPT_REAL(
“n <- max(.arg6)
df <- data.frame(.arg1,.arg2,.arg3,.arg4,.arg5)
pc <- prcomp(df, scale = TRUE)
as.numeric(pc$x[,n])
“,
SUM([人口当たりビール消費量]),
SUM([人口当たり酒消費量]),
SUM([人口当たり焼酎消費量]),
SUM([人口当たりワイン消費量]),
SUM([人口当たりウィスキー消費量]),
2
)
—————————————-
+ メジャーバリューをクロス表として表示します。
+ 県名(Pref)を列に、メジャーバリューを行にドラッグします。
+ 作成した計算式prcomp1.prcomp2 は表計算となりますので、次を使用して計算でPrefを指定してください。
+ V10.2からの個別の凡例を利用してメージャーごとに異なる配色をしてみましょう。
+ prcomp1 で並べ替えをしてみます。
左から 人口当たりの焼酎消費量、人口当たりの酒酎消費量、PC1 の値となります。
PC1が高い(緑色)では人口当たりの焼酎消費量の色が濃い傾向に、PC1が低い(青色)では人口当たりの酒消費量の色が濃い傾向にあるようです。
また焼酎の消費量と酒の消費量の色のグラデーションが相反することから、焼酎の消費量と酒の消費量は反比例の関係にあるようです。
これにより、主成分1は高いと焼酎消費量が高く、低いと酒消費量が高いことを示す指標となることが分かります。
主成分2(PC2)についてはワインの消費量とグラデーションが似ているので、ワインの消費量の関与が大きいといえます。
Rでみたbiplotのベクトルの方向からもこの傾向はわかります。
+ 次に主成分を使って散布図を作成します。
+ prcomp1 を列に、prcomp2を行に、表計算で次を使って計算でPrefを指定します。
+ 色にメジャーバリューを利用し、 prcomp1 とprcomp2を使用します。
+色に個別の凡例を使用して、透明度を低く設定すると、prcomp1の配色とprcomp2 の配色を重ねることができます。prcomp1の高低によって緑と青が変化し、prcomp2 の高さによって赤が濃くなります。
例えば、鹿児島、宮崎、熊本は主成分1が強く、焼酎消費量が高い傾向、
新潟、秋田、石川は逆に焼酎消費量が低く、日本酒消費量が強い傾向があります。
東京、山梨、北海道は 主成分1が強く、ワイン消費量が強い傾向があります。
バブルの大きさに焼酎消費量を使ってみると面白いかもしれません。
Rのbiplotの結果も併せてダッシュボードにするとよりわかりやすいかもしれません。
以上のように、ビール、酒、焼酎、ワイン、ウイスキー消費量など、複数の項目指標があるときこれらの傾向を1つの図の中に表示することはできませんが、
これらの特徴をうまく抽出する主成分を2つ作り出すことで、主成分1と主成分2の2次元の散布図を作ることができ、各都道府県の類似性を可視化することができました。
RのbiplotのベクトルがTableauでも表示できればよいのですが、良い手が浮かばず、どなたかアイディアがあればご教示ください。
以上、参考になれば幸いです。
よろしくお願いします。
追記: 成分ベクトルをTableauで表現する方法について
Rで主成分分析を行うと、biplotを使って成分のベクトルを表示させることができます。これをTableauでも表現してみたいと思います。
Tableauから動的にRのスクリプトを呼ぶのではなく、Rで計算した主成分の結果をデータセットに追加し、それを静的にTableauから表示するという形になってしまうのですが、ご了承ください。
この例では、都道府県の各アルコールの消費量の偏差値のデータを読み込みます。
Rの Import DatasetからFrom CSVで読み込みます。
以下のようなRスクリプトが実行されます。
> AlcoholJapan <- read_csv(“C:/tmp/AlcoholJapan.csv”)
> View(AlcoholJapan)
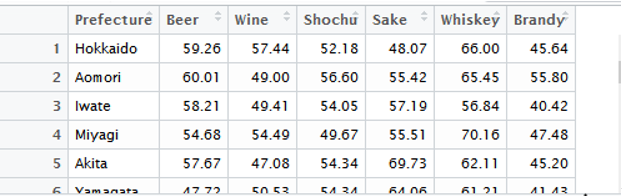
データフレームとして格納します。
> data <- as.data.frame(AlcoholJapan)
1列目をデータ名として定義します。
> row.names(data) <- data[,1]
実データは2列目から7列目となります。
> data = data [,2:7]
主成分分析を行った結果をresultに入れます。
> result = prcomp(data,scale=TRUE)
Rで描画します。
> biplot(result)
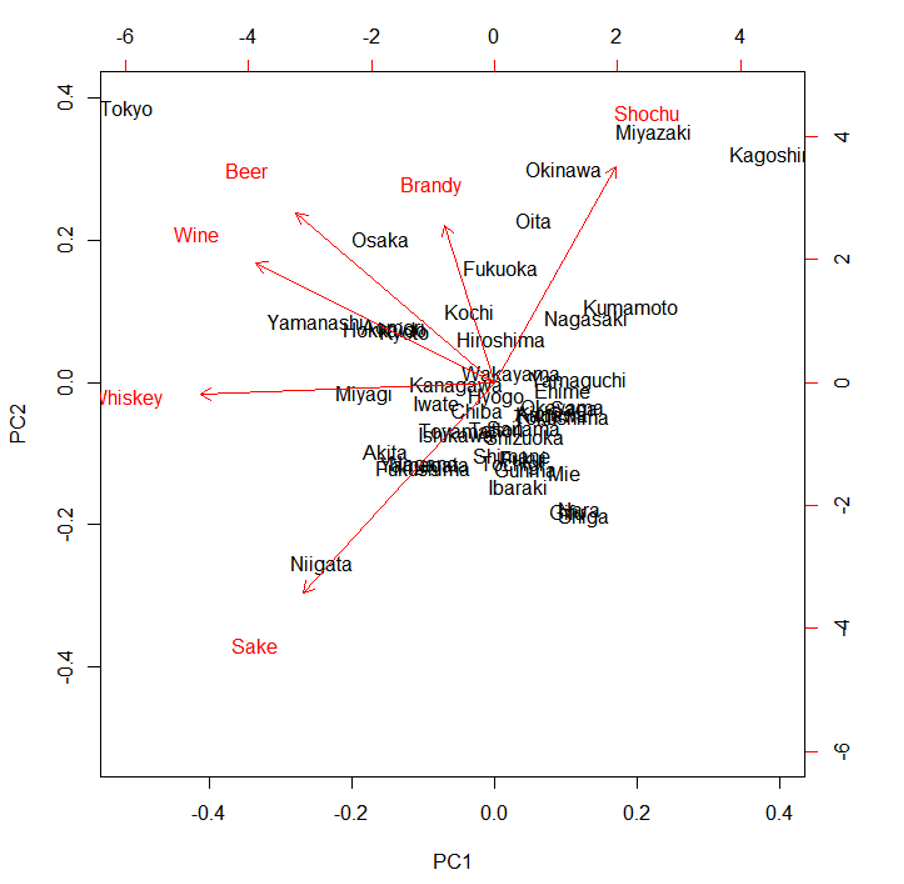
第1主成分、第2主成分を変数に格納し、オリジナルデータの横に連結します。
> x1 <- result$x[,1]
> x2 <- result$x[,2]
>data1 <- cbind(data,x1,x2)
これをCSVに書き出します。
>write.csv(data1,”c:/tmp/pricompAlcoholJapan.csv”)
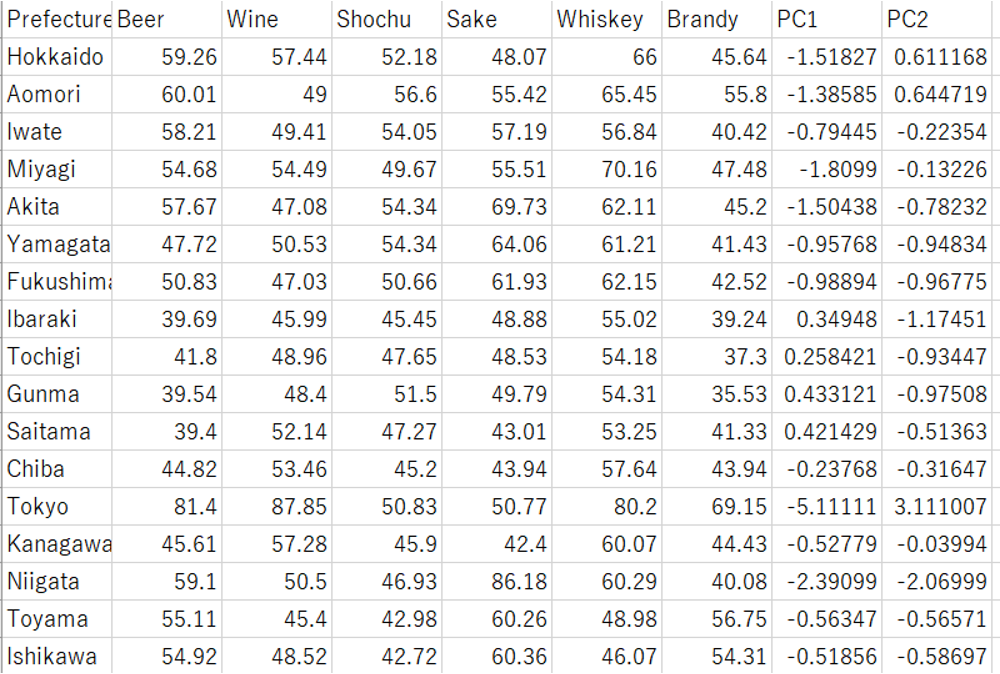
これだけで第1主成分と第2主成分をX,Y軸に取る散布図が書けるのですが、もう一ひねりして成分のベクトルを加えてみます。
主成分分析の結果 result を表示して、第1主成分と第2主成分のデータをEXCELに転記します。(テキストで保存してEXCELからインポートするとよいかと思います)
> result
Standard deviations:
[1] 1.4422628 1.1820604 1.0579559 0.8559347 0.6679182
[6] 0.4739216
Rotation:
PC1 PC2 PC3 PC4
Beer -0.4076188 0.42601812 -0.2435827 -0.493872361
Wine -0.4899263 0.30017216 0.3397780 0.488143267
Shochu 0.2503558 0.54216439 0.3934388 -0.499823739
Sake -0.3934619 -0.52684153 -0.1738223 -0.465389439
Whiskey -0.6048846 -0.02984634 0.2907859 -0.005001642
Brandy -0.1021932 0.39498128 -0.7454218 0.226649785
PC5 PC6
Beer 0.590633994 0.01626403
Wine 0.009152746 -0.56218516
Shochu -0.470308955 -0.13255708
Sake -0.339892960 -0.45309711
Whiskey -0.298848011 0.67774056
Brandy -0.474383644 0.03850561
0から起点とする放射を描くため、Pathの情報を加えて、以下のようにデータを加工します。
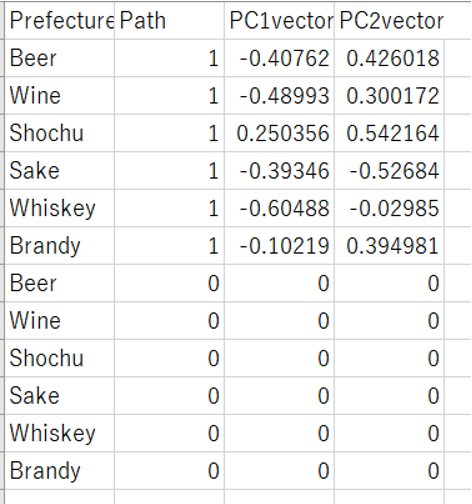
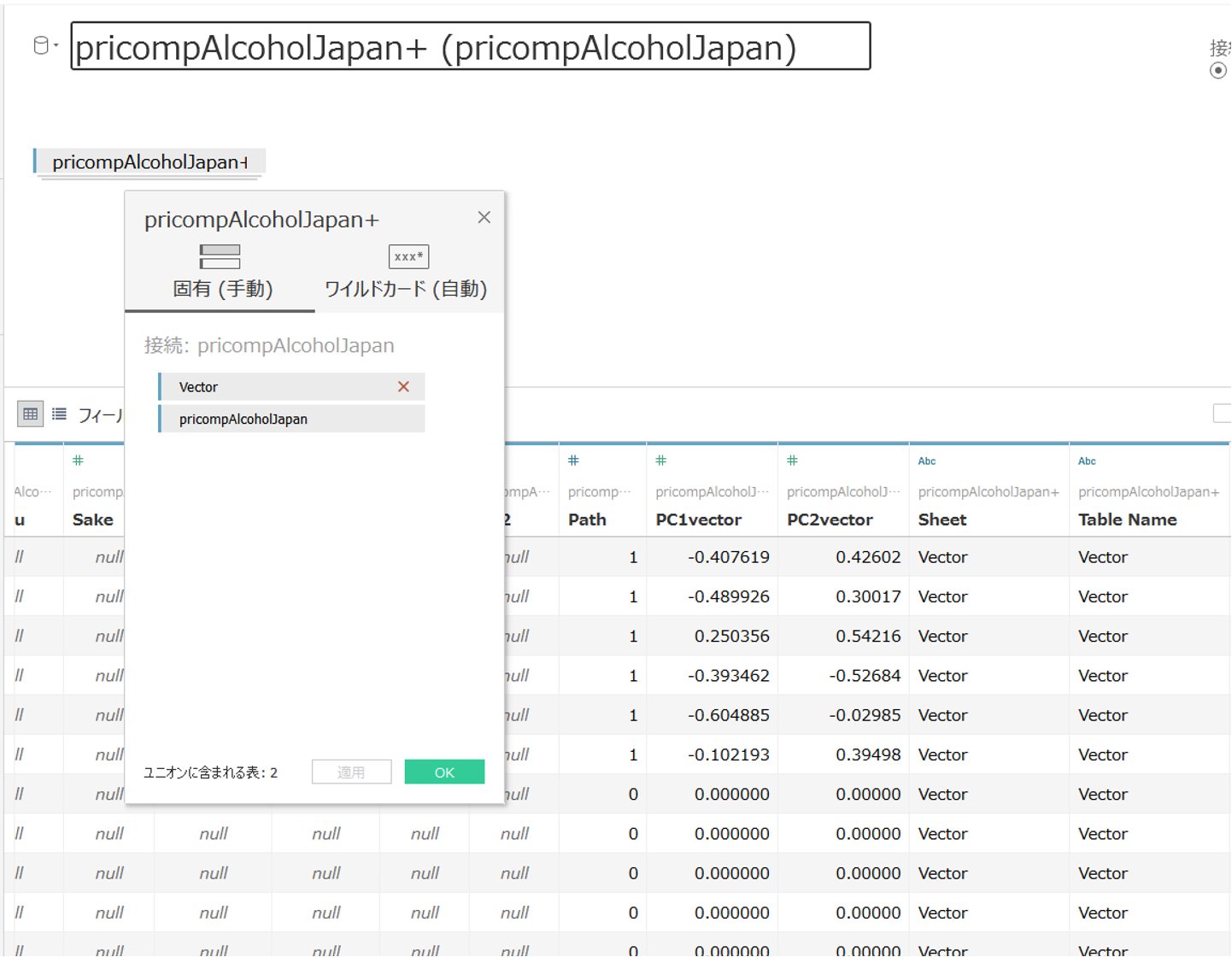
2つのデータをユニオンします。アルコール科目の列名もPrefecture としておくのがポイントです。
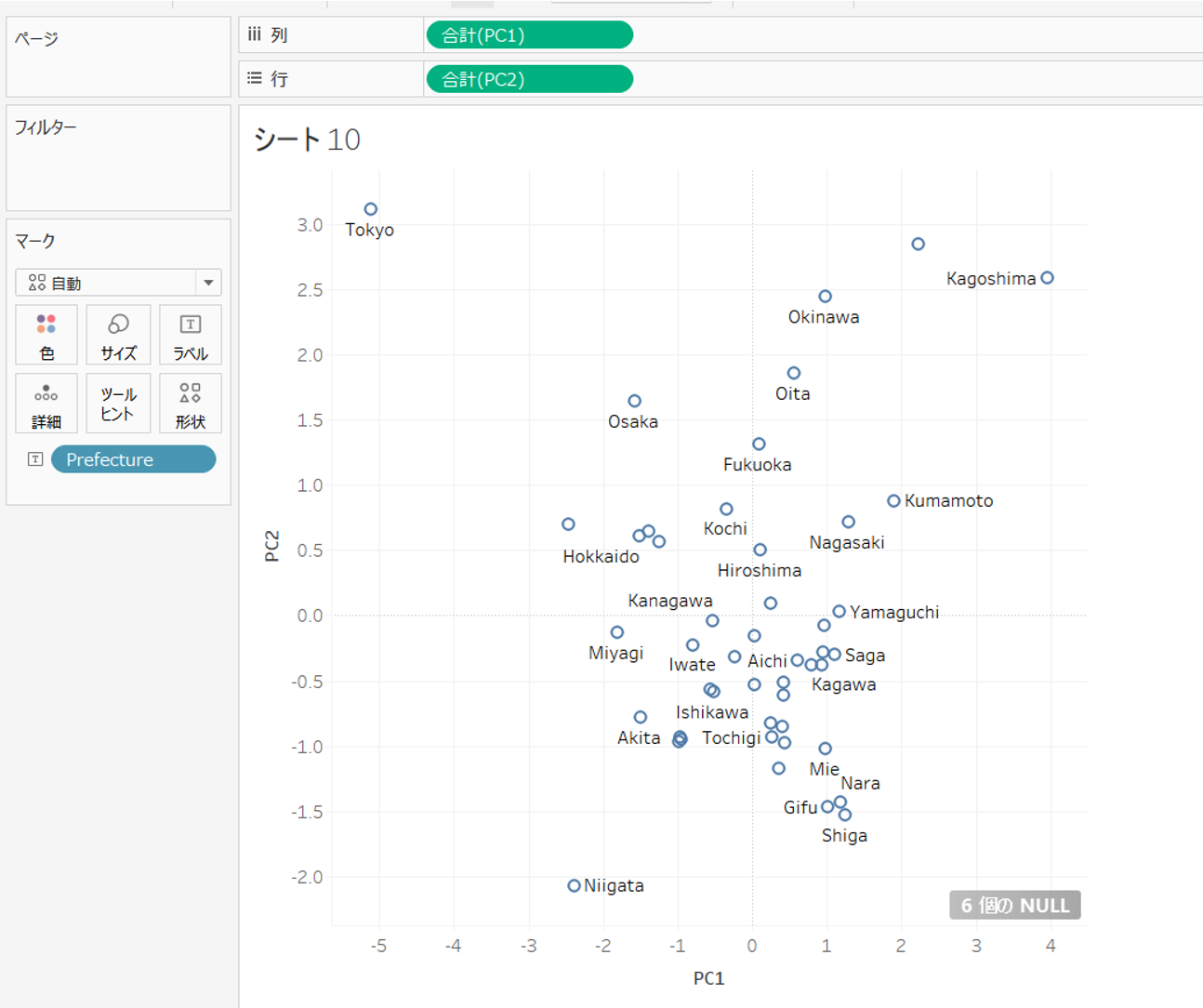
まずはPC1とPC2で散布図を描きます。
次にベクトルのPC1とPC2を列、行にドラッグします。
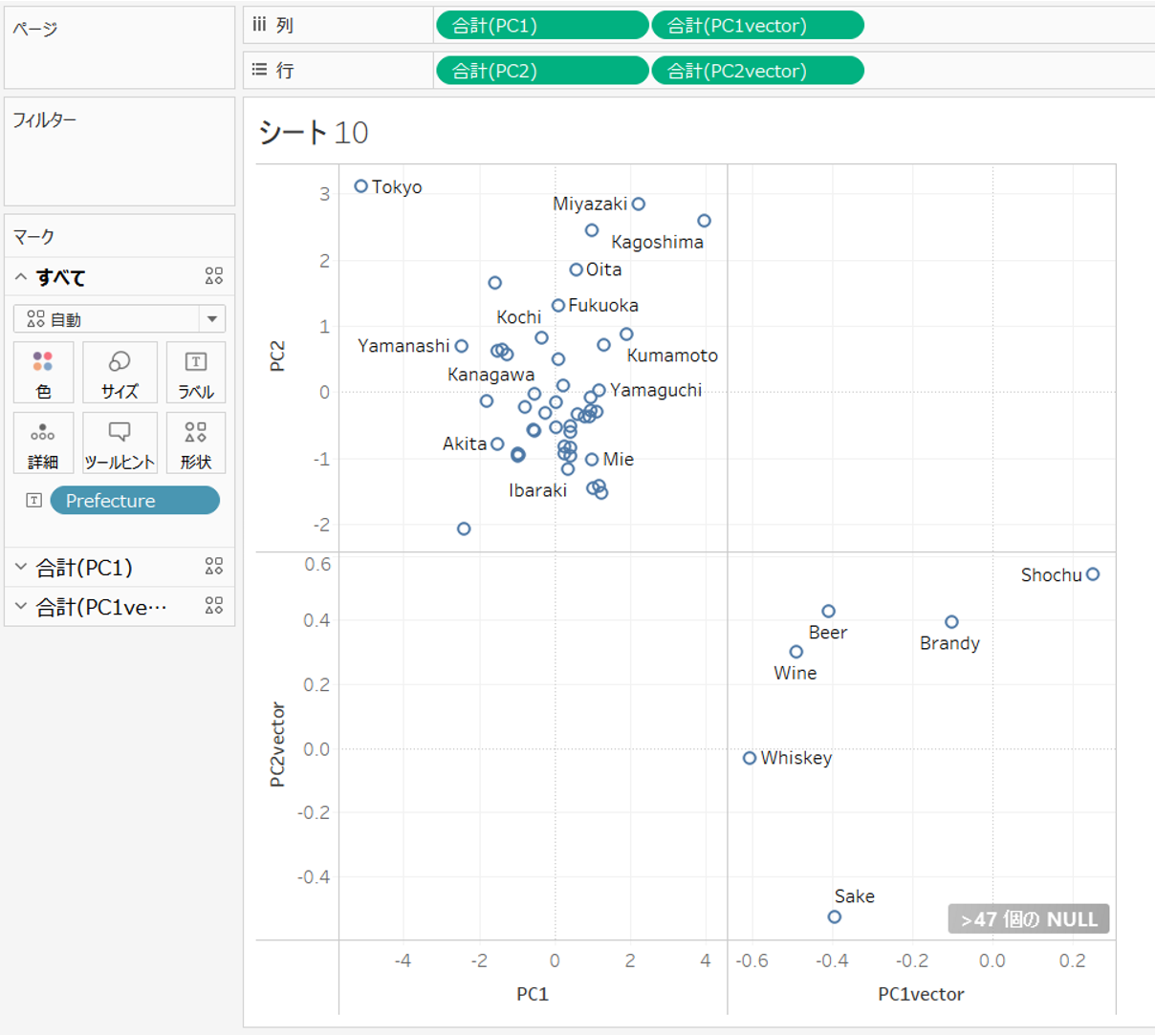
表示形式を線に、パスにPathを追加します。
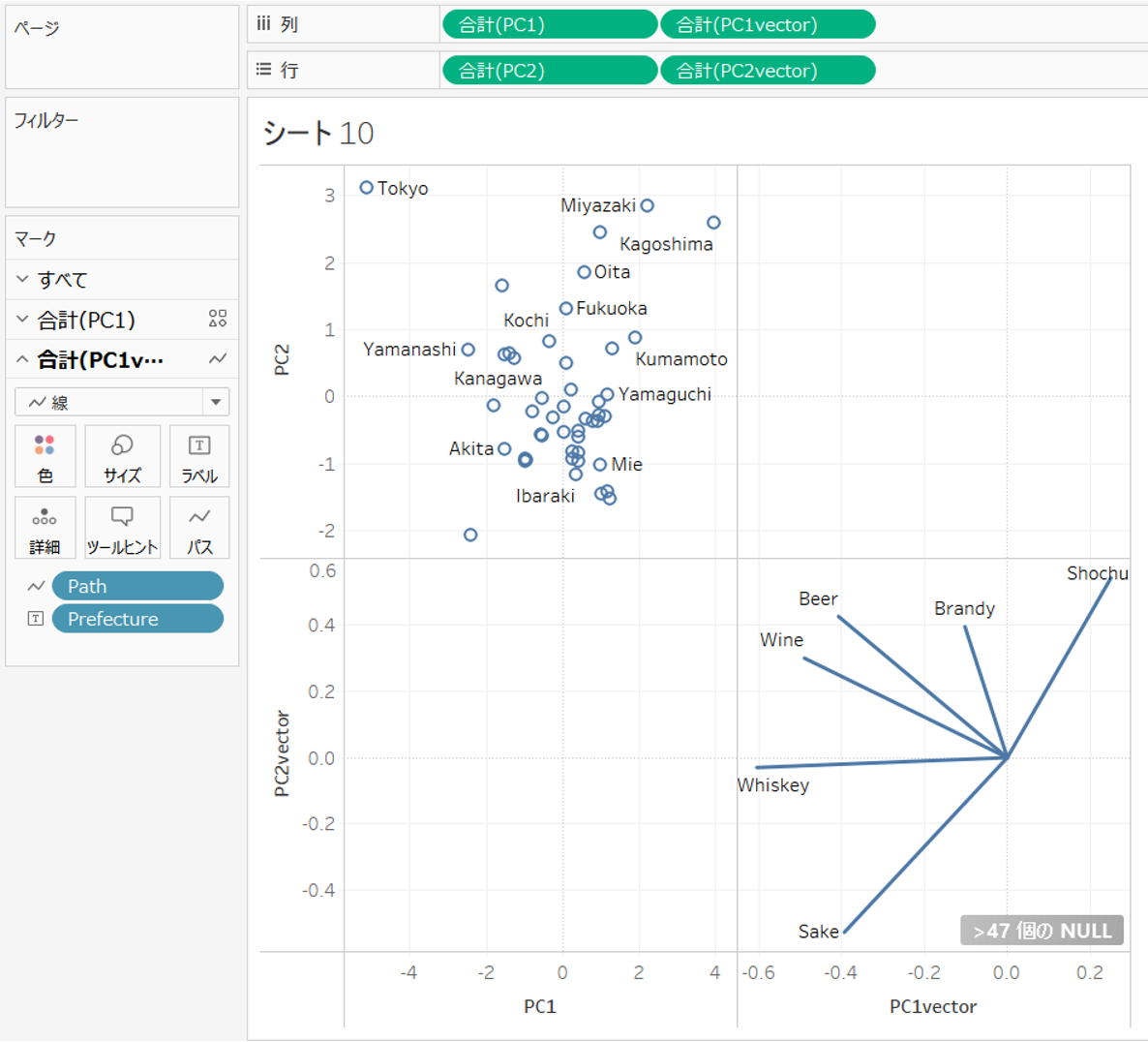
二重軸を設定し、色やサイズを調整します。
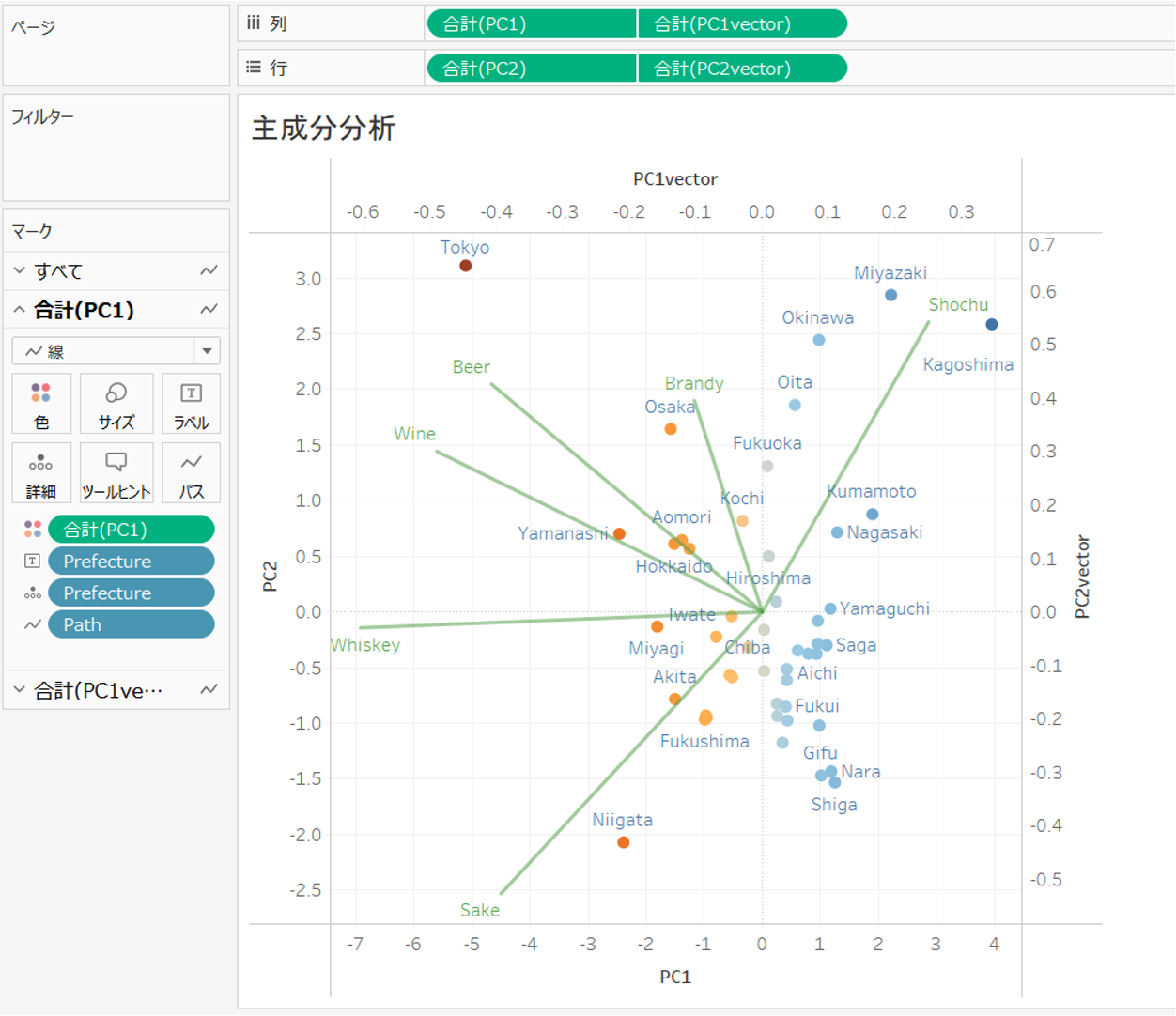
Tableau Public はこちらから参照ください。






